Understanding how to find the slope of a line is an important skill in mathematics. The slope helps us describe how steep a line is on a graph. It tells us how much the line goes up or down as we move along the x-axis (the horizontal line). This concept is used in many fields, including physics, engineering, and economics. In this article, we will explore what slope is, how to calculate it, and why it is useful.
To find the slope of a line, we use a special formula. This formula uses the coordinates of two points on the line. By knowing these points, we can find out how steep the line is. In the following sections, we will break down the steps to calculate the slope, explain the slope formula in detail, and provide examples to help you understand the concept better.
What is Slope?
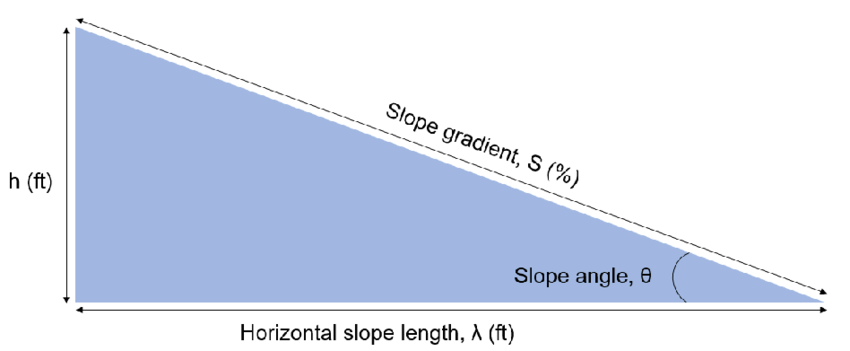
Slope is a measure of the steepness of a line. It tells us how much the line rises or falls as we move from left to right. In simpler terms, slope is the ratio of the change in the y-coordinate (vertical direction) to the change in the x-coordinate (horizontal direction). When we have two points on a line, we can calculate the slope using these points.
The slope can be positive, negative, zero, or undefined. A positive slope means the line goes up as we move from left to right. A negative slope means the line goes down. A zero slope means the line is flat, and an undefined slope occurs when the line is vertical.
The Slope Formula
The formula for finding the slope is:
m=(y2−y1)(x2−x1)m = \frac{(y_2 – y_1)}{(x_2 – x_1)}m=(x2−x1)(y2−y1)
Here, m is the slope of the line, (x1, y1) are the coordinates of the first point, and (x2, y2) are the coordinates of the second point.
Breaking Down the slope Formula
- (y2 – y1): This part calculates the change in the y-coordinates. It tells us how much the line rises or falls.
- (x2 – x1): This part calculates the change in the x-coordinates. It tells us how far we move horizontally.
To find the slope, we subtract the y-coordinate of the first point from the y-coordinate of the second point and do the same for the x-coordinates.
Steps to Find the Slope
Here are the steps to find the slope of a line:
- Identify the Points: First, find two points on the line. Each point will have an x-coordinate and a y-coordinate. For example, let’s say our points are (2, 3) and (5, 7).
- Label the Points: Assign the first point as (x1, y1) and the second point as (x2, y2). In our example, (x1, y1) = (2, 3) and (x2, y2) = (5, 7).
- Use the Slope Formula: Substitute the coordinates into the slope formula:
m=(y2−y1)(x2−x1)=(7−3)(5−2)m = \frac{(y_2 – y_1)}{(x_2 – x_1)} = \frac{(7 – 3)}{(5 – 2)}m=(x2−x1)(y2−y1)=(5−2)(7−3) - Calculate the Change: Simplify the expression:
m=43m = \frac{4}{3}m=34
So, the slope of the line is 43\frac{4}{3}34.
Example of Finding Slope
Let’s find the slope of a line that passes through the points (1, 2) and (4, 6).
- Identify the points: (x1, y1) = (1, 2) and (x2, y2) = (4, 6).
- Substitute the points into the formula: m=(6−2)(4−1)=43m = \frac{(6 – 2)}{(4 – 1)} = \frac{4}{3}m=(4−1)(6−2)=34
- The slope of the line is 43\frac{4}{3}34.
Different Types of Slope
- Positive Slope: A line that rises from left to right has a positive slope. For example, the line connecting (1, 1) and (3, 4) has a slope of 3−13−1=1\frac{3 – 1}{3 – 1} = 13−13−1=1, indicating it rises.
- Negative Slope: A line that falls from left to right has a negative slope. For example, the line between (1, 4) and (3, 2) has a slope of 2−43−1=−1\frac{2 – 4}{3 – 1} = -13−12−4=−1, indicating it falls.
- Zero Slope: A horizontal line has a slope of zero. For example, the line between (2, 3) and (5, 3) has a slope of 3−35−2=0\frac{3 – 3}{5 – 2} = 05−23−3=0.
- Undefined Slope: A vertical line has an undefined slope. For example, the line connecting (2, 1) and (2, 4) has a slope that cannot be calculated because the x-coordinates are the same, leading to division by zero.
Using Slope in Real Life

The concept of slope is not just for math class; it has many practical applications. Here are a few examples:
- Construction: Builders use the slope to create ramps, roofs, and roads. A proper slope ensures safety and efficiency.
- Economics: In economics, the slope is used to understand trends in data. For example, it can show how the price of a product changes as demand increases.
- Physics: In physics, slope helps to analyze motion. For instance, a steep slope indicates a fast speed, while a flat slope indicates a slow speed.
Conclusion
Finding the slope of a line is a simple yet powerful mathematical skill. By understanding the slope formula and how to apply it, you can analyze various situations, whether in math, science, or real-life applications. Knowing the slope helps us understand how lines behave and relate to each other.
In summary, slope is all about how steep a line is. By using two points, we can easily calculate it using the formula m=(y2−y1)(x2−x1)m = \frac{(y_2 – y_1)}{(x_2 – x_1)}m=(x2−x1)(y2−y1). Remember, the slope can be positive, negative, zero, or undefined, depending on the line’s direction. With practice, you’ll be able to find the slope of any line confidently.
FAQs
Q: What is the slope of a line?
A: The slope of a line measures how steep it is and is calculated as the change in y divided by the change in x.
Q: How do you calculate slope using coordinates?
A: Use the formula m=(y2−y1)(x2−x1)m = \frac{(y_2 – y_1)}{(x_2 – x_1)}m=(x2−x1)(y2−y1), where (x1, y1) and (x2, y2) are two points on the line.
Q: What does a positive slope mean?
A: A positive slope means the line rises from left to right, indicating an increase in y as x increases.
Q: What does a negative slope indicate?
A: A negative slope indicates that the line falls from left to right, meaning y decreases as x increases.

